Veda2.0 Released!
|
Elastic Demand and Investment Cost
|
|
16-01-2014, 06:03 PM
Hi,
We have been looking into elastic demand results and what that means it terms of investments, cost saved, etc. It appears that by imposing the ED on energy service, the reductions in energy service given price increases almost always result in proportional reductions in capital investment in end use technologies, such as vehicles, cooling units, heating units, etc. Ideally, you can probably imagine that long-term elasticity in service demand will lead to some reduction in capital investments in end use technologies. For example, people might buy fewer cars if they travel less. However, it is also more than likely that people will buy almost the same # of cars except that they will just drive less for each car. This example is even more obvious when you think about heating and cooling technologies. People will most likely still buy one heating unit and one cooling unit for each home, except that they will use each less frequently when fuel price increases. Thus the current kind of modeling results that we are seeing: less service demand from ED translates to the same proportional reduction in investment in end use technology is probably incorrect (over stating the benefits in reducing cost of mitigation). We've thought about a few options to address this, such as making capacity variable flexible (which makes little to no difference in an optimization model since the model always like to use the maximum amount), exogenously adjusting the capacity factor to a lower value (which is difficult to do since we don't know how much service demand will be reduced a prior), and a few other tricks, but nothing seems to be like a good solution. I wonder if any of you have thought about this problem before? Do you identify this as a "problem" with the ED? If not, why (maybe we are misusing it)? if yes, how do you deal with this issue? I've read a bunch of TIMES/MARKAL papers using ED, and nobody seems to suggest this as a problem. I suspect people just report the results without thinking too much about it, or we are using it wrong, or people have figured out other ways to solve this? Your thoughts on this would be greatly appreciated. -Sonia
23-01-2014, 03:12 AM
Thanks for this good question Sonia.
I created an example with a possible solution. Of course, it has imperfections, but looks like a feasible starting point. Example Model Too many little things to describe, so I recorded a video instead.
Amit: Yes, your solution might be useful. Here is a slightly different alternative to your ED-AF-Red, which produces basically identical results for the example, but includes also an easy way of setting a lower limit for the utilization of each technology. uploads/30/Scen_ED-AF-BLUE.rar (requires TIMES v3.4.8 or above) However, the consistency of these approaches is not so obvious to me. When imposing the capacity constraint (and without applying a policy), the marginals of the demand will be reduced considerably when moving towards lower demands. Consequently, the Baseline prices are no longer valid in the policy scenarios. I think you would need to apply the binding capacity constraints already in the Base scenario in order to get consistent Base prices for the subsequent policy scenarios. I saw this problem clearly when I raised the investment costs in your example and then ran again the Baseline and the modified elastic demand scenario, but the latter without the high price scenario. The Baseline results were correctly reproduced in the ED scenario, but the marginals for the demand were much lower in the ED scenario, just because the capacity-constraints were already active.
23-01-2014, 12:31 PM
Antti, as usual, you have come up with a very elegant solution. Your attribute-based scenario does seem to replace my two UCs. I would pick blue over red
 . .About the demand price - it has basically been shared with the UC. If I add the shadow price of the capacity constraint, then I get an exact match with the Base case demand marginal. Shouldn't the ED variables have come in if the prices were really not valid? I have not understood the use of AFA(LO). I am sure you have thought of a case with several freely competing technologies, but I don't see how it would work.
23-01-2014, 12:49 PM
About prices: Your investment costs were so small that the ED variables came in even if the Base prices were not consistent, but too high. In a real world example with cars, the investments would dominate the Base year prices, and you would thus most probably end up having no demand elasticity effect, unless you would apply the (binding) capacity constraints already in the Base scenario, to get consistent prices. AFA: I was thinking that AFA(LO) would prevent investing in the cheapest available technology without actually using it, just to satisfy the capacity constraint. With AFA(LO), all capacity would have to be used at least to a minimum utilization level.
23-01-2014, 02:06 PM
OK, all clear, thanks.
Sonia: it would be great to have an update on this thread (if and) when you try this approach.
Hi Amit and Antti,
Thanks for your thoughtful response and proposed solutions!! I will definitely take a look and report back! (I am quite slow in moving through my to-dos, my apology in advance). -Sonia
There
was also the general question about whether the reduced investments due elastic
demands may actually lead to a systematic underestimation of mitigation costs. I
am not sure whether that can be a serious problem, but below are just some basic thoughts
based on my understanding:
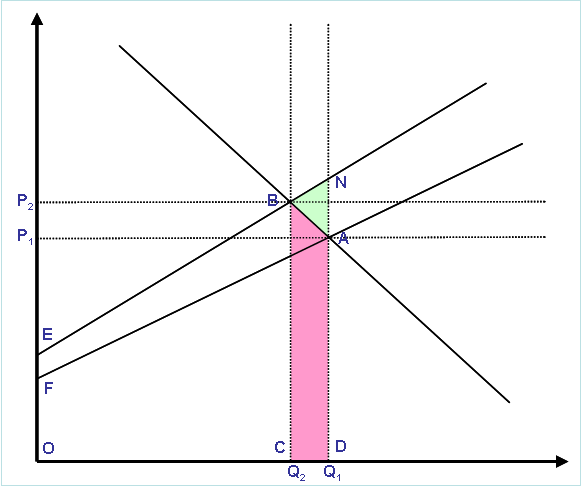
As far as I can see, the ED approach used in TIMES works in the same way as other partial equilibrium models based on maximizing the total surplus. For a single demand, the mechanism can be illustrated by the following simplified graph:
Assume that in the Baseline, the supply-demand equilibrium is established at point A with demand Q1 and price P1. The total supply costs correspond to the area within the polygon ADOF. When a mitigation policy is applied, the supply curve shifts upwards, and if we assume that the demand is not elastic, the new equilibrium is obtained at point N with total supply costs NDOE, and a surplus loss NAFE. The total costs are thus in this case ADOF + NAFE = NDOE. But if we assume that the demand is elastic, the new equilibrium is at point B with demand Q2 and price P2. The total supply costs now correspond to BCOE, and the surplus loss is BAFE. Therefore, in this case the total costs correspond to ADOF + BAFE = BCOE + ABCD = ADOEB). And this is what TIMES uses in the objective function. In the ED case the total costs ADOEB thus include a notable surplus loss component ABCD (marked in red in the graph) in addition to the direct supply costs BCOE. The surplus loss is included in the TIMES objective function and in the reporting parameters (e.g. Cost_ELS). Compared to the non-elastic demand case (NDOE), the total costs are reduced only by the amount of ABN (marked in green) in the ED case. In other words, it seems to me that even if when using ED the reduced demand level may lead to a proportional reduction in investment costs, the total mitigation costs are reduced much less, because the additional surplus loss compensates most of the decrease in the supply costs. But perhaps this conclusion is not so relevant to the question presented? Hi Antti, Thanks for the solutions and the supply-demand equilibrium figure. The figure, and how the theory was implemented in the model, are correct. The total system costs with ED is the area BCOE + plus the cost of demand reduction (loss of consumer welfare, area ABCD in red). So the overall savings with ED compared with no ED is ABN in green. What's imperfect, in my view, is the way it was implemented by us (the modelers), and the lack of empirical studies to properly implement them. As we raised earlier, when the price of a commodity (say, fuel) increases, consumers will reduce service demand by (1) reducing the operation of the equipment (thus saves fuel costs), or (2) forging the purchase of a new equipment (thus saves fuel and technology costs). Consumers will make this tradeoffs based on the marginal costs of reducing the last unit of service demand, plus some unobserved utilities (e.g. the convenience of keeping a vehicle as an option). Previously without any modification, the model always chooses (2) since
it is the least-cost option. The modification that you proposed, essentially
forces the model to choose (1). I think it is a fine solution for most building
technologies (e.g. water heater, space cooling, space heating, lighting). So we
plan to go ahead and play with the new modification in our model residential
and commercial sectors. (Still note that the selection of AFA (Lo) is also
arbitrary, and I suspect that AFA (Lo) may become binding if AFA(Lo) is
smaller than COM_VOC and you force the capacity to be the same as the
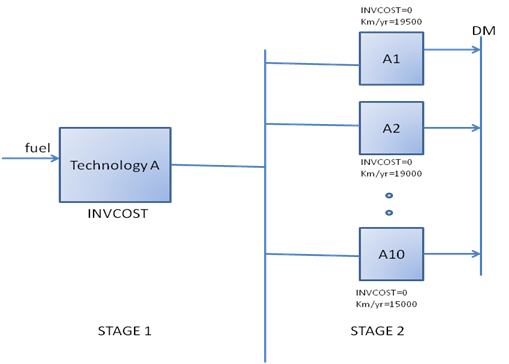
BAU?) However, because you force the capacity under ED the same as the BAU, you are taking option (2) off the table. Therefore I think this implementation is not desirable with technologies that consumers do have the option to reduce the number of vehicle purchases at the aggregated level). The other solutions that Richard Loulou proposed (in email), is to model a 2-stage decision: each vehicle is now represented by a two-stage diagram. The first stage has a single technology that bears the investment cost and the fuel(s) input(s). The second stage is a series of technologies each with zero INVCOST but a different value for the parameter that represents the kilometers traveled per year (and perhaps also a different value for the annual fixed cost FIXOM, since maintenance would be somewhat reduced if fewer km are traveled each year). This way consumers have both options: when the price of a commodity (say, fuel) increases, consumers will reduce service demand by (1) reducing the operation of the equipment (thus save fuel costs), or (2) forging the purchase of a new equipment (thus save fuel and technology costs). Consumers will make this tradeoffs based on the marginal costs of reducing the last unit of service demand, plus some unobserved utilities (e.g. the convenience of keeping a vehicle as an option). Richard's solution allows consumers to make this trade offs based on the marginal cost of reducing (1)(Stage 2) or (2)(Stage 1). (As a side comment, it however does not include the utility of owning a vehicle despite low utilization rate (e.g. in case of emergencies, bad weather, convenience, or just to look cool. Not owning a car has disutilities (costs) associated with it which makes consumers less likely to choose this option if both options have the same marginal cost). Another downside of this option is that you have to add many dummy technologies for for each vehicle technology, and the choices are discrete. Therefore it is probably not feasible to have this kind of structure for all vehicle types, class. sizes, in all years, etc. Now back to the nice figure you drew. Again the theory is correct, but
the way the supply curve is constructed is less idea if we only directly or
indirectly allow consumers to choose either (1) or (2) (whether we as modelers
reflect the true choices the consumers make and the costs of the tradeoffs),
and the selection of the ED values from the literature (whether the study
design that the ED values were calculated matches is the correct slope we want to
intercept our supply curves) are the real challenges. Best, -Sonia
02-02-2014, 10:31 AM
Hi Sonia,
I am very glad that you consider some of the solutions for improving the model responses to price changes viable, although there are still challenges remaining. Concerning my example solution, you are of course right about the choice of AFA(Lo), which should reflect the maximum reduction in capacity utilization considered realistic. Note also that in that example you could even define an elasticity for both the activity and capacity demand, such that both demands would have a price response. Alternatively, you could define a relationship between the activity and capacity demands, such that, for example, if the activity demand reduces by 2%, the capacity demand would be reduced by 1% (whereas in the original example the capacity demand did not decrease at all, and without any modification they would both reduce by 2%). Concerning Richard's two-stage decision solution, if you can implement an example based on that approach, could you post the example here? I would be quite interested to see how it really works.
07-02-2014, 03:13 PM
Hi Antti, sorry for the late reply. (just got back from New Delhi with limited internet access). Richard's solution is posted below. I think he probably wouldn't mind me posting it here: FROM RICHARD LOULOU: 1. Indeed, when service demand (call it DM) is reduced (due to its own price elasticity), TIMES (as currently used by us and probably by all users), will never choose to reduce kilometers traveled while maintaining capacity. This is because there is a rigid, exogenous relationship between capacity and kilometers traveled (e.g. each car travels 20,000km/year). Hence the model will either reduce capacity (relative to Base Case), or switch to some other technology that travels fewer kilometers par year. However, there is no such alternate technology in the database, so the only way to reduce DM is to reduce capacity. 2. One way to provide more flexibility to the model is illustrated in fig.1, where each vehicle is now represented by a two-stage diagram. The first stage has a single technology that bears the investment cost and the fuel(s) input(s). The second stage is a series of technologies each with zero INVCOST but a different value for the parameter that represents the kilometers traveled per year (and perhaps also a different value for the annual fixed cost FIXOM, since maintenance would be somewhat reduced if fewer km are traveled each year). Example : 10 steps, a 2.5% reduction in km/yr, and a 2% FIXOM reduction, at each step: Tech A (original vehicle): 20,000 km/yr FIXOM=3000$/yr Tech A1: 19500 km/yr, FIXOM=2960$/y Tech A2: 19,000 km/yr, FIXOM=2920$/yr ... Tech A10: 15,000 km/yr, FIXOM=2600$/yr The model could now choose a mix of decisions consisting in reducing investment (by decreasing the investment variable in the first stage) and switching to some alternate technology in the list of ten. 3. The above is mechanically OK, but not at all guaranteed to reproduce real life consumer choices. Indeed, in real life, the car owner has her own utility function governing the arbitrage between reducing her car travel and relinquishing her vehicle altogether. Such arbitrage is not easily represented in optimization models. (This difficulty is quite similar, and related to the one involving switching from personal travel to mass transit). 4. In some demand segments, the situation is more clear-cut. As noted by Sonia, home dwellers will always keep a space heating device, but are amenable to reducing the indoor temperature. In such segments, one could fix the VAR_INV variable in the first stage to its value in the Base Case, so that the only way to reduce DM is now to switch to some alternate technology in the list of the second stage. 5. These quick and dirty ideas should be mulled over, and perhaps tested... Figure 1. Two stage representation of a single vehicle
I'm trying to understand Sonia's and Antti's explanation of the system cost with Elastic Demand, based upon Antti's graph.
I understand that the total supply costs in the case of elastic demand is BCOE, but I'm not sure I follow that the cost of surplus loss is ADCB (the pink region). Consumer surplus is measured as the area under the demand curve that is above the equilibrium price, while the producer surplus is typically the area under the price line and above the supply curve. So I'm not sure I follow how the bottom part of the pink region is included in the elasticity cost (ELASTCOST), since it includes the area below the original supply curve -- the cost of supplying the energy in the original scenario (and thus is not surplus). Are we saying that we are counting the loss of all benefits that consumers derive (i.e. the entire area under the demand curve)? any additional information elucidating this would be helpful thanks, Chris TIMES maximizes the net total surplus of consumers and producers. It does that by minimizing the total costs = supply costs + elasticity costs. As I said in my earlier post referring to the graph, in the elastic demand case the total surplus decreases by the amount of BAFE compared to the Baseline. The total costs should thus increase by that amount compared to the Baseline. From the graph you can immediately see that the elasticity costs must therefore be ABCD, which is the integral of the demand price function over the demand reduction. See the TIMES documentation, Part I, Section 6.2.2 Formulating the TIMES equilibrium for details on the formulation for maximizing the net total surplus. To see that the elasticity costs associated with the total surplus loss must indeed be ABCD, one could also employ the fact that the total surplus is equal to the integral of the demand price function (from zero to the equilibrium demand) minus total supply costs.
07-03-2014, 02:27 PM
Antti,
thanks for the detailed reply. Here's what I do understand: I understand that Supply costs of base case is ADOF and elastic case is BCOE. I understand that the the surplus in base case is AFX and elastic case is BEX (I extended the demand curve to intersect the y-axis at point "X". I understand the difference in surplus between base case and elastic case is BAFE. I also understand that the total system cost in elastic case is equal to baseline supply cost + surplus loss (ADOF + BAFE), this also happens to be equal to elastic supply cost (BCOE) + ABCD. I guess I'm used to thinking in terms of minimizing system cost and not maximizing surplus so this is why it seems more logical to me if the total system cost in the elastic case were instead equal to the elastic supply cost + surplus loss (BCOE + BAFE)? Probably this is why I'm having some trouble just accepting it. On a related topic, I'm also trying to understand the real-world significance of the difference in system cost between the base and elastic cases. The times documentation says "That difference is of course, the negative of the difference between the net total surpluses of the two scenario runs". The difference between the two surpluses is the BAFE. And so the difference between the base and elastic supply costs is ABCD. But what does this number (ABCD) mean? I can see it is equal to the loss of consumer utility from the demand reduction (Q1 to Q2), but it is not surplus (since it ignores the cost that consumers would pay for this utility). Thoughts on how to interpret this value would be appreciated. Chris 
07-03-2014, 06:06 PM
In my opinion, "loss in consumer utility" is a the correct interpretation for ABCD, just like you stated. I don't see why you are seeking for some other interpretation? Using the term "utility" for short, we can write: ∆(surplus) = ∆(utility) – ∆(supply costs) Because ∆(utility) is negative whenever the price increases, it is obviously an important component of the total surplus loss. And the total system costs in TIMES can be simply expressed as:
Of course, I would also appreciate further insights from others. |
|
« Next Oldest | Next Newest »
|
Users browsing this thread: 1 Guest(s)